Have you ever tried to create an asymmetrical design, and gotten stuck wondering just where to start? Christine Jablonski suggests that you look to the mathemeticians for ideas.
Say the word math in a room full of creatives, and you could very well find yourself facing a chorus of protestations along the lines of “I don’t do math,” or “I’m not a numbers person.” But math provides a mechanism to understand relationships and solve problems—the very things we do every time we sit at our looms. I, for one, was shocked when I learned that my beloved Fibonacci sequence, which has served me so well through so many projects, is one of the first examples given in many calculus texts.

One of the well-known spirals that illustrates the Fibonacci sequence is the seed pattern in a sunflower. Photo by Chris Greninger on Unsplash
Fibonacci Sequence
Leonardo Bonacci, better known simply as Fibonacci, was an Italian mathematician who, in 1202, popularized a specific succession of numbers. Interestingly, this sequence had been referenced in Indian mathematics as early as 200 CE, but apparently Fibonacci had a better publicist. The sequence is such that each number is the sum of the preceding two numbers: 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13, 8+13=21, and so on. Designs based on this order tend to be aesthetically pleasing, probably because we see these patterns every day. Tree branching systems, the arrangement of a flower’s petals and seed heads, the spiral of a seashell or a pine cone’s scales are just a few examples of how the natural world manifests this rule.
I based the first pattern I ever published on the Fibonacci sequence. To someone nervous about sending her first effort out into the world, it was a safe place to start, and by all accounts, the project was a success. Since then, this sequence has provided a foundation for many of my designs, although I’ve adapted it for weaving along the way.
When applying the Fibonacci sequence in weaving, you not only have numbers of units (ends, inches, or repeats) to work with, but you also have numbers of colors at your disposal. In my experience, choosing Fibonacci numbers for ends or picks that are different from the number of colors in the colorway makes a project more visually dynamic.
For example, when designing the warp for the towels in Photo 1, I chose to repeat three Fibonacci numbers (2, 3, and 5) as doubled ends on a rigid-heddle loom with four colors (natural, orange, yellow, and hot pink). While the width repeats are consistent, the colors do not often repeat with the same widths, which keeps the overall pattern more active than a simple repeat.

Left: Christine repeated three Fibonacci numbers to design her towel stripes. Right: You can mix up the Fibonacci numbers for a dynamic design, such as the one Christine developed for these placemats. All photos by Christine Jablonski unless otherwise noted
There’s no rule that says you must use the Fibonacci numbers in order. For the placemats in Photo 2, I used six numbers (1, 2, 3, 5, 8, and 13) doubled as loops in the threading sequence over four colors (white, turquoise, light brown, and purple). However, I also assigned white as a single loop between each of the other colors, making the final sequence 2, 1, 3, 1, 5, 1, 8, 1, 13, 1 . . . with each color except for white threaded with a different number of ends over the course of the warp.
You can also just throw caution to the wind, pick a handful of Fibonacci numbers, and thread them in any order as I did with the stash-buster project in Photo 3. Fibonacci numbers get large quickly (21, 34, 55, 89 . . .), which is a terrific way to manage large color blocks and narrow stripes—especially if your stash contains a lot of some colors and a little of others.

Even when you use a wide variety of numbers from the Fibonacci sequence in a piece, their relationships to each other will pull your design together.
The color order for this warp was somewhat random, based on how much of each color I had available and, honestly, which colors I thought looked better next to each other on the loom. I used Fibonacci numbers to determine the width of the stripes: 34, 2, 55, 8, 2, 34, 13, 13, 2, 13, 89 (ends, not loops).
The Cantor Set
One day, in a not-so-subtle hint that I might consider branching out from Fibonacci, my engineer husband introduced me to the Cantor set. Georg Cantor was a German mathematician in the 1800s who is considered the father of Set Theory. I won’t pretend to know what that means, but in the Cantor set, a segment (let’s say a warp) is divided into 3 equal units (widths). Then, each end unit is divided into thirds, and each of those end units is also divided into thirds (and this goes on to infinity). How might you use a Cantor Set in weaving? Let’s say you have a 27-inch-wide warp (or a warp with 27 repeats across) but aren’t sure how to sequence the colors. Applying the Cantor set would give you the design below.
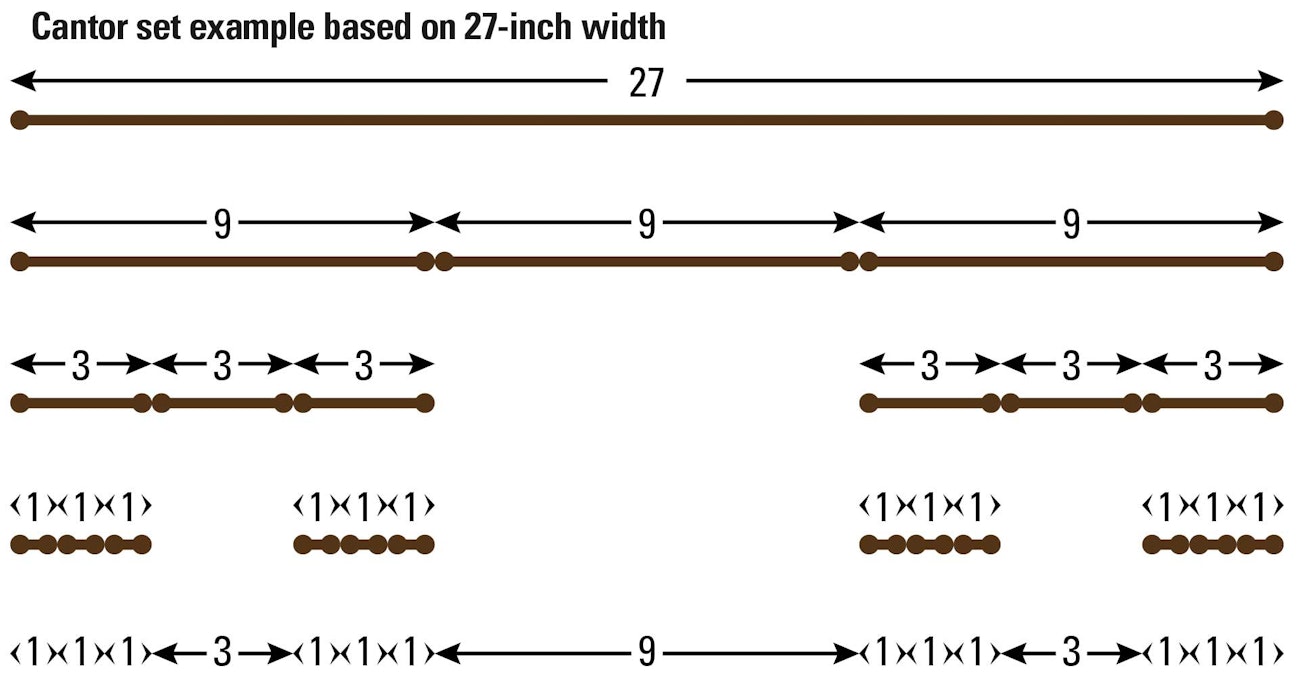
This means the final warping would be: 1-1-1-3-1-1-1-9-1-1-1-3-1-1-1.
In Photo 4, you can see that I segmented my warp into three sections: the center blue and what had been equal lengths of natural on either side. Then the natural widths were divided by three and the far right and far left segments of those two sections were divided by three again, leaving natural in the middle, bordered by black and blue stripes.

Left: Christine started by dividing her warp into three equal parts and then applied principles of the Cantor set to the three sections. Right: Move your stripes around as Christine did if you are looking for asymmetry in a cloth.
Many designs based on this mathematical sequence are possible! You could start at the bottom with 1s (repeats, inches, sets of 10 ends) and then build up. Alternatively, once you have your stripe sequence, you can move the stripes around, as I did in the towel in Photo 5 when I shifted the three small stripes from the right-hand side to the left, making the design asymmetrical. To my eye, it’s a little unexpected and a lot more interesting.
This is only a cursory glance at the power of math and its intersection with design, but I hope the message is clear—math isn’t the problem; it’s more likely a solution. Approaching numerical sequences as relationships and ways to solve problems gives you an incredible tool that you can manipulate to create amazing patterns. I bet Fibonacci and Cantor would have designed some great projects!
Read more about keys to asymmetrical design in the Summer 2024 issue of Handwoven.
CHRISTINE JABLONSKI is a weaver and fiber artist who is absolutely convinced that had her high school math teachers related numbers to weaving, she would have paid a lot more attention in class.

